Timbre and Plate Vibrations Ken Ellis How do the back and top of an autoharp affect the timbre of the sound? The obvious answer is that these plates filter the string vibrations in a manner that depends on the type of wood and the bracing and soundhole geometry. However, there is more to it than that. The back and top plates actually add complex tones to the sound that enhance the timbre. In this issue we will look at the physical mechanism that generates these complex tones. The engineers and scientists out there may be wondering how a string that vibrates at a specific set of harmonics can generate tones that are different from those harmonics. The wave equations that describe vibrations are linear equations. So one would expect that an autoharp, or any acoustic instrument, would be a linear system. To appreciate this statement, let me explain what a linear system is. Linear Systems A linear system treats each input frequency as an independent component. The intensity of the output of a linear system at any given frequency is only dependent on the intensity of the input at that same frequency. So for example, the 100 Hz output of a linear system depends only on the intensity of the input at 100 Hz. The input intensity at 101 Hz has no effect at all on the 100 Hz output. Many systems encountered in science and engineering are linear, often by design. For example, electrical and optical systems are usually designed to make any nonlinearities so small that they can be ignored. This allows us to accurately model these systems as linear. Linear systems are relatively easy to model and analyze, and there are many analysis tools available. Non-linear systems, on the other hand, are usually very difficult to analyze. Scientists and engineers like linear systems. So the equation describing vibrations is a linear equation. Are acoustic instruments linear systems when it comes to producing sound? Pretty much anything you'd want to know about sound is in Lord Rayleigh's “The Theory of Sound”. If you can find it. If you can understand it when you find it. Here is what Lord Rayleigh says in Section 99: “It is important to remember that in response to a simple harmonic force, the system will vibrate in general in all its modes”, and “but any normal component, which has a node at the point of application, will not be excited”. In other words, when a driving force having a single frequency is applied to a mechanical system it stimulates all of the natural frequencies of the system, except those which have a node right at the point where the force is applied. So in general we should not expect an acoustic instrument, or any mechanical system subject to vibrations, to act like a linear system. Try This At Home You can hear how a single string can stimulate other vibrational modes for yourself on your own autoharp. I'll wait here while you go get one. . . . Welcome back. Pluck any string, then immediately stop that string from ringing by holding your finger tip against it. You should hear other strings ringing. This is what happens. The string that you plucked starts the body vibrating. The vibrating body then starts shaking the ends of all of the strings, causing the strings to vibrate at their natural frequencies. These new string vibrations then cause the body to vibrate and continue to produce sound, even though you are preventing the original string from vibrating with your finger tip. And the cycle repeats. For this experiment the body of the autoharp is basically a feedback loop for the strings. In this case, “all the modes” mentioned by Rayleigh include the vibrational modes of the other strings as well as the vibrational modes of the body. Most of what you hear are the string harmonics that have the same frequencies as the harmonics of the string that you plucked. But there are more than just these string harmonics present. Transient and Steady-State Modes We can get some additional insight into what happens when the strings stimulate the top and back of an autoharp from the venerable Benade. In Chapter 10 of “Fundamentals of Musical Acoustics”, a much more approachable tome than Rayleigh's, we find that when an instrument plate is driven by a single frequency (e.g. each harmonic of a vibrating string), the plate's response is a combination of the free vibrational modes of the plate (i.e. the modes you get when you tap it) and the driving frequency. The free vibrational modes decay quickly compared to the driving frequencies (harmonics) produced by a string. If you are a fan of differential equations you may recall that the general solution for the damped harmonic oscillator has transient and steady state parts. The transient part describes the free vibrational modes and the steady-state part describes the response to the driving frequencies. Experimental Confirmation We can see these two types of vibrations in spectrograms of notes played on an autoharp. 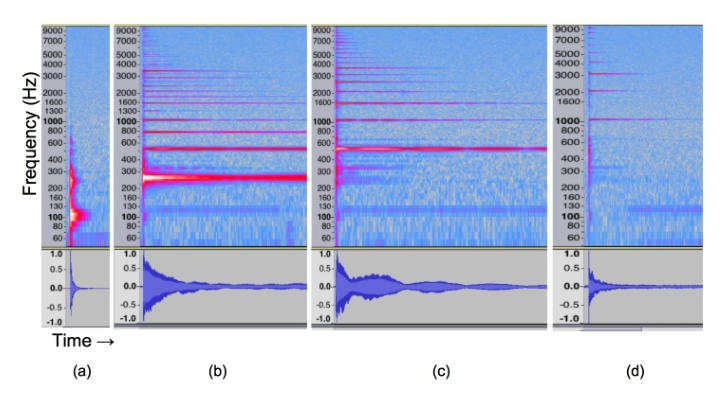A spectrogram shows the loudness of a note as a function of both time and frequency. Figure 1 depicts the spectrograms of a body tap tone and three notes: C4, C5, and C6. C4 is middle C and the others are one and two octaves higher, respectively. The horizontal axis of a spectrogram represents time and the vertical axis represents frequency. The color represents the loudness of the indicated frequency as a function of time after the string was plucked. The hotter colors indicate a louder sound. Remember, the strings vibrate at the fundamental frequency of the note (261, 523, and 1046 Hz for C4, C5, and C6, respectively) and at harmonics that are basically multiples of the fundamental frequency. The spectrogram in Figure 1(a) is of the sound produced by tapping the back of an autoharp. This spectrogram has a peak at about 100 Hz, which is the frequency at which the air plug in the soundhole vibrates for the autoharp measured. The back and top modes also contribute, producing a spread from roughly 60 to 700 Hz. Notice the short duration of the body vibrations. If you look carefully at the left side of the string spectrograms in Figures 1(b), (c), and (d), you will see what looks like a faint copy of the body vibrations between 60 and 700 Hz. This is from the top, back, and air plug vibrational modes from Figure 1(a) as they are stimulated by the string vibrations. The 100 Hz air plug mode is especially noticeable. You can see by the short time duration that these are transient modes, which decay quickly to nothing. The various body modes are not in the same proportion to each other in the four spectrograms. To quote Lord Rayleigh again, “The magnitude of each component thus depends on two things: (1) on the situation [position] of its nodes with respect to the point at which the force is applied, and (2) on the degree of agreement between its own proper period [or frequency] and that of the force.” The relative levels of the body modes depend on how well each mode couples to the string harmonics, which in turn depends on the shapes of the plate modes and where each string is fastened to the body. Therefore, the effect of the body vibrations on the timbre will be slightly different for each note. Notice that the spectrograms show that the autoharp does act like a linear system after the transients die down. This is the implicit assumption made when analyzing vibrating mechanical systems with a linear model, that the transients are very short on the time-scales of interest. Transients will always be important in determining the sound of an autoharp because it is a plucked instrument. From Vibrations to Timbre Now you might be asking yourself “Self, how can the transient modes have a significant effect on the sound when the steady-state modes are longer and louder?” Two reasons. First, while the steady-state string harmonics are higher in intensity than the body transients, they are also narrower in frequency. If we look at the total sound energy over all frequencies, we see that the transients for C6 contain about one third of the total sound energy. So it is reasonable to suppose that the transients can have a noticeable effect. Second, we know from Pierre Schaeffer's experiments in the 1950's that the transients at the beginning of a tone have a disproportionate influence on the timbre of the sound. Schaeffer's experiments, described in Daniel Levitan's book, related timbre to the initial transients. He recorded several instruments on tape, edited out the transient of each note, and played back the result. He found that it was almost impossible to identify what instruments had made the notes, or to distinguish one instrument from another. This suggests that the initial transients of an instrument are the dominant factor in determining timbre. You can see from the spectrograms that the frequency spectra of the initial transients are different from the steady-state spectra for each note. Schaeffer also showed that if you splice the initial transients from one instrument onto the steady-state of the same note from another instrument, you get mixed results. It may sound more like the instrument from which the initial transients were taken, or it may sound like nothing you have ever heard before. Timbre and Geometry The degree to which the timbre depends on the top and back plates is a function of the plate thickness and stiffness. A thick plate has more mass than a thin plate and so a given amount of string energy will move it less (cause it to vibrate with a lower amplitude) than a thin plate. A stiffer plate (and thicker plates are also stiffer plates) will reflect more of the acoustical energy that attempts to enter the plate than a not-so-stiff plate. With less acoustical energy entering the plate, the vibration amplitudes will also be less. So a thicker, stiffer plate will not only produce less sound for a given picking force but also have less of an effect on the timbre of the instrument. So the bottom line is this. When a string vibrates, it causes the plates to vibrate at all of the frequencies that do not have nodes at the string anchor points. This adds frequencies to the sound that do not exist in the string itself. The loudness and balance of the added frequencies depends on the type of wood, the plate thicknesses, and the positions and profiles of the braces on the plates. In as much as the soundhole affects the way that the top vibrates, it too can affect the frequencies introduced by the top. These added frequencies, although short in duration, contribute significantly to the timbre of the autoharp, making the sound dependent on both the species of woods used and the autoharp design. References Benade, A. H., “Fundamentals of Musical Acoustics”, Dover Publications, New York, 1990. Levitan, Daniel J., “This is Your Brain on Music: The Science of a Human Obsession”, Plume, New York, 2007. Rayleigh, J. W. S., “The Theory of Sound”, Dover Publications, New York, 1945.

Autoharp Acoustics